Following:
http://www.roma1.infn.it/teongrav/leonardo/bh/bhcap3.pdf
http://www.roma1.infn.it/teongrav/leonardo/bh/bhcap4.pdf
$J = $ angular momentum
$M = $ mass
$a = \frac{J}{M}$
$\Sigma = r^2 + a^2 cos^2 \theta$
$\Delta = r^2 - 2 M r + a^2$
$x = \sqrt{r^2 + a^2} sin \theta cos \phi$
$y = \sqrt{r^2 + a^2} sin \theta sin \phi$
$z = r cos \theta$
$ds^2 = -dt^2 + \Sigma (\frac{1}{\Delta} dr^2 + d\theta^2) + (r^2 + a^2) sin^2 \theta d\phi^2 + \frac{2 M r}{\Sigma} (a sin^2 \theta d \phi - dt)^2$
$= -(1 - \frac{2 M r}{\Sigma}) dt^2 + \frac{\Sigma}{\Delta} dr^2 + \Sigma d\theta^2 + (r^2 + a^2 + \frac{2 M r a^2}{\Sigma} sin^2 \theta) sin^2 \theta d\phi^2 - \frac{2 M r a sin^2 \theta}{\Sigma} dt d\phi$
$g_{tt} = -(1 - \frac{2 M r}{\Sigma})$
$g_{rr} = \frac{\Sigma}{\Delta}$
$g_{\theta\theta} = \Sigma d\theta^2$
$g_{\phi\phi} = (r^2 + a^2 + \frac{2 M r a^2}{\Sigma} sin^2 \theta) sin^2 \theta$
$g_{t\phi} = -\frac{2 M r a sin^2 \theta}{\Sigma}$
$g_{\mu\nu} = \pmatrix{
g_{tt} & 0 & 0 & g_{t\phi} \\
0 & \frac{\Sigma}{\Delta} & 0 & 0 \\
0 & 0 & \Sigma & 0 \\
g_{t\phi} & 0 & 0 & g_{\phi\phi}
}$
To find the inverse of $g_{\mu\nu}$, find the inverse of $\tilde{g}_{ab} = \pmatrix{ g_{tt} & g_{t\phi} \\ g_{t\phi} & g_{\phi\phi}}$:
$det( \tilde{g}_{ab} ) = g_{tt} g_{\phi\phi} - g_{t\phi}^2$
$ = -(1 - \frac{2 M r}{\Sigma})(r^2 + a^2 + \frac{2 M r a^2}{\Sigma} sin^2 \theta) sin^2 \theta - (\frac{2 M r a sin^2 \theta}{\Sigma})^2$
$ =
-r^2 sin^2 \theta
-a^2 sin^2 \theta
- \frac{1}{\Sigma} 2 M r a^2 sin^4 \theta
+ \frac{1}{\Sigma} 2 M r^3 sin^2 \theta
+ \frac{1}{\Sigma} 2 M r a^2 sin^2 \theta
+ \frac{1}{\Sigma^2} 4 M^2 r^2 a^2 sin^4 \theta
- \frac{1}{\Sigma^2} 4 M^2 r^2 a^2 sin^4 \theta
$
$ = (
-r^2
-a^2
+ \frac{1}{\Sigma} 2 M r (-a^2 sin^2 \theta + r^2 + a^2)
) sin^2 \theta$
$ = (
-r^2
-a^2
+ \frac{1}{\Sigma} 2 M r (a^2 cos^2 \theta + r^2)
) sin^2 \theta$
$ = (-r^2 - a^2 + 2 M r) sin^2 \theta$
$ = -\Delta sin^2 \theta$
So $\tilde{g}^{ab} = \pmatrix{
g^{tt} & g^{t\phi} \\
g^{t\phi} & g^{\phi\phi}
} = -\frac{1}{\Delta sin^2 \theta} \pmatrix{
g_{\phi\phi} & -g_{t\phi} \\
-g_{t\phi} & g_{tt}
}$
$g^{tt} = -\frac{1}{\Delta} (r^2 + a^2 + \frac{2 M r a^2}{\Sigma} sin^2 \theta)$
$g^{t\phi} = -\frac{2 M r a}{\Delta \Sigma}$
$g^{\phi\phi} = (1 - \frac{2 M r}{\Sigma}) \frac{1}{\Delta sin^2 \theta}$
$= (\Sigma - 2 M r) \frac{1}{\Sigma \Delta sin^2 \theta}$
$= (r^2 + a^2 cos^2 \theta - 2 M r + a^2 - a^2) \frac{1}{\Sigma \Delta sin^2 \theta}$
$= (r^2 - a^2 sin^2 \theta - 2 M r + a^2) \frac{1}{\Sigma \Delta sin^2 \theta}$
$= (\Delta^2 - a^2 sin^2 \theta) \frac{1}{\Sigma \Delta sin^2 \theta}$
So $g^{\mu\nu} = \pmatrix{
-\frac{1}{\Delta} (r^2 + a^2 + \frac{2 M r a^2}{\Sigma} sin^2 \theta) &
0 &
0 &
-\frac{2 M r a}{\Delta \Sigma} \\
0 & \frac{\Delta}{\Sigma} & 0 & 0 \\
0 & 0 & \frac{1}{\Sigma} & 0 \\
-\frac{2 M r a}{\Delta \Sigma} &
0 &
0 &
\frac{1}{\Delta sin^2 \theta} (1 - \frac{2 M r}{\Sigma})
}$
Killing fields:
$\mathcal{L}_x g = 0$
$g_{\mu\nu,\alpha} x^\alpha + g_{\mu\alpha} {x^\alpha}_{,\nu} + g_{\alpha\nu} {x^\alpha}_{,\mu} = 0$
Since $g_{\mu\nu,t} = g_{\mu\nu,\phi} = 0$, we get Killing field vectors:
$k^\mu = (1,0,0,0)$ and $m^\mu = (0,0,0,1)$
Energy at infinity $= -k_\mu u^\mu = -g_{t\mu} u^\mu = -u_t$
Angular momentum per unit mass $= -m_\mu u^\mu = -g_{\phi\mu} u^\mu = -u_\phi$
TODO coordinates singularity at $\Delta = 0$
Horizon of $\Delta = 0$
$r^2 - 2 M r + a^2 = 0$
...has solutions:
$r = \frac{1}{2} ( 2 M \pm \sqrt{ 4 M^2 - 4 a^2})$
$r = M \pm \sqrt{M^2 - a^2}$
...has real solutions only for $M^2 - a^2 \ge 0$
$a^2 \le M^2$
For $a^2 = M^2$ defining an extremal black hole
Let $\Delta = (r - r_+)(r - r_-)$
For $r_\pm = M \pm \sqrt{M^2 - a^2}$
Therefore the coordinate singularity $\Delta = 0$ can be represented as $r = r_\pm$.
Radial surface to $\Theta = r - constant = 0$:
normal: $n_\mu = \Theta_{,\mu} = (0,1,0,0)$
normal norm: $n_\mu n_\nu g^{\mu\nu} = \frac{\Delta}{\Sigma}$
So when $r = r_\pm$ we have $\Delta = 0$ and $|n| = 0$, which is a null hypersurface.
$r=r_+$ is the outer horizon
$r=r_-$ is the inner horizon
$|n| = \frac{\Delta}{\Sigma}$ looks like ...
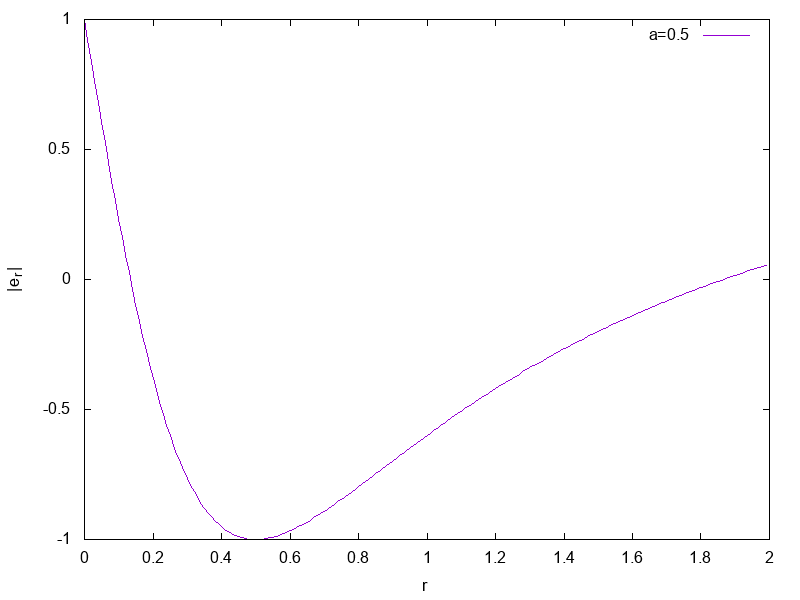
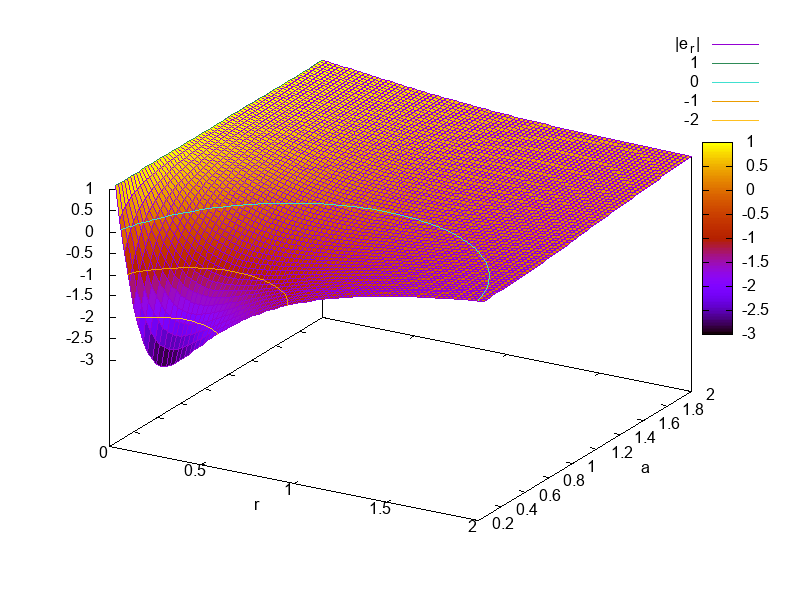
$r > r_+$ is timelike, $r_+ > r > r_-$ is spacelike, $r_- > r$ is timelike.

