Rivers at the equator are more twisty than those further North or South.
Trees at the equator are more twisty than those further North or South.
The spacetime further N or S of the equator is twisting more than at the equator.
Maybe in nature there's a certain amount of 'twist' required.
And in the N and S, twisting comes from spacetime.
But in the equator twisting has to be accomodated for in the structure of plants and rivers.
so how much does the spacetime twist ...

That's the question of - what's the geodesic acceleration of geodesic pointing around the rotation axis ... for coordinates the $\theta$ polar angle, $\phi$ the angle around ...
We use the geodesic equation $\dot{u}^i = -{\Gamma^i}_{jk} u^j u^k$
And the anholonomic-normalized, spherical-surface connections:
${\Gamma^\theta}_{\phi\phi} = -\frac{1}{r} cot(\theta) = -{\Gamma^\phi}_{\phi\theta}$.

So our equation of its acceleration, expanded, is
$\dot{u}^i = -{\Gamma^i}_{\theta\theta} u^\theta u^\theta - {\Gamma^i}_{\theta\phi} u^\theta u^\phi - {\Gamma^i}_{\phi\theta} u^\phi u^\theta - {\Gamma^i}_{\phi\phi} u^\phi u^\phi$
So our vector us pointing around the circle... with no up/down component ... so it has $u^\theta = 0, u^\phi = 1$ ...
So plug in and this simplifies to $\dot{u}^i = -{\Gamma^i}_{\phi\phi} u^\phi u^\phi$.
so $\dot{u}^\theta = -{\Gamma^\theta}_{\phi\phi} = \frac{1}{r} cot(\theta)$ (the amount it is pulled N/S by the geodesic).
And $\dot{u}^\phi = -{\Gamma^\phi}_{\phi\phi} = 0$ (the amount it is pulled E/W by the geodesic).
So the twisting up/down is by $\frac{1}{r} cot(\theta)$ for $\theta$ the polar angle ... 0 = north pole, 90' = equator, 180 = south pole.



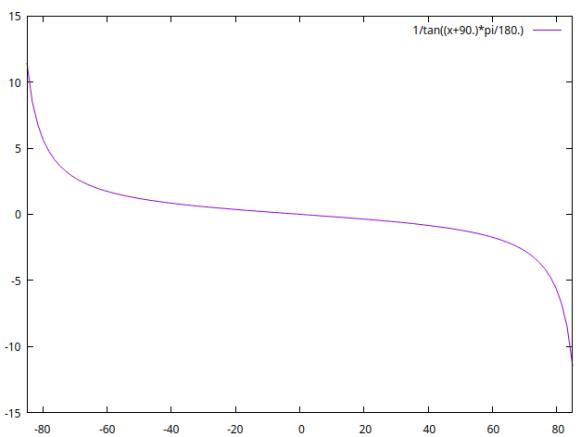
Likewise the parallel-propagation of a vector along the equator is given by...
${P^i}_j (\phi_L, \phi_R) = exp(-\int_{\phi_L}^{\phi_R} {\Gamma^i}_{\phi j})$

${P^i}_j (\phi_L, \phi_R) = exp \left[ \begin{matrix} 0 & \frac{\Delta \phi}{r} cot(\theta) \\ -\frac{\Delta \phi}{r} cot(\theta) & 0 \end{matrix} \right]$

${P^i}_j (\phi_L, \phi_R) = \left[ \begin{matrix} cos \left( -\frac{\Delta \phi}{r} cot(\theta) \right) & sin \left( -\frac{\Delta \phi}{r} cot(\theta) \right) \\ sin \left( -\frac{\Delta \phi}{r} cot(\theta) \right) & cos \left( -\frac{\Delta \phi}{r} cot(\theta) \right) \end{matrix} \right]$